문제 출처
programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
문제 설명
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
제한 사항
- W, H : 1억 이하의 자연수
입출력 예
| W | H | result |
| 8 | 12 | 80 |
입출력 예 설명
입출력 예 #1
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

✨문제풀이
문제만 이해하면 푸는 건 그렇게 어렵지 않은 문제이다.
가로가 8, 세로가 12인 직사각형의 대각선은 아래와 같이 4개의 2X3 사격형의 대각선으로 쪼갤 수 있다.
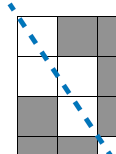
이렇게 대각선이 그어진 부분을 최소 단위로 쪼개고 금이 그어져 사용할 수 없는 사격형의 개수를 계산하면 되는 문제이다.
1) 쪼개어진 사각형의 크기는 최대 공약수로 구할 수 있다.
가로와 세로를 최대 공약수로 나눈 몫이 사각형의 크기가 된다. 8과 12의 최대공약수는 4이고, 4를 나눈 몫은 각각 2와 3이 된다. 따라서 가로 8, 세로 12는 가로 2, 세로 3인 직사각형으로 쪼갤 수 있다.
-> divisor라는 변수에 가로와 세로 중 작은 값을 넣어주고 -1씩 해주며 가로와 세로 값에 공통으로 나누어지는 값을 찾아 나누어 준다. 더이상 나누어지지 않을 때까지 반복해서 나누어준다.
2) 쪼개어진 사각형 안에서 사용할 수 없는 사각형의 개수를 계산한다.
가로 사각형 개수와 세로 사각형 개수를 더한 값에서 1을 빼주면 된다. 가로2, 세로3인 사각형 안에서 금이 그어진 부분은 2 + 3 - 1로 계산할 수 있다.
-> 최대 공약수로 나눈 몫을 이용해 계산해 준다
w * h : 전체 사각형 개수
num1(가로) + num2(세로) - 1 : 쪼갠 사각형에서 금이 그어진 사각형 개수
w / num1(가로) : 금이 그어진 대각선부분에서 쪼갠 사각형 개수
'코딩테스트' 카테고리의 다른 글
| 프로그래머스 - 삼각 달팽이 (레벨2, swift) (0) | 2020.12.18 |
|---|---|
| 프로그래머스 - N개의 최소공배수 (레벨2, swift) (0) | 2020.12.13 |
| 프로그래머스 - 큰 수 만들기 (레벨2, swift) (0) | 2020.12.09 |
| 프로그래머스 - 타겟 넘버 (레벨2, swift) (2) | 2020.11.30 |
| 프로그래머스 - 소수 찾기 (레벨2, swift) (0) | 2020.11.26 |